RANDOM STUFF ----- [TOP]

Mathematical Trends on the ArXiv

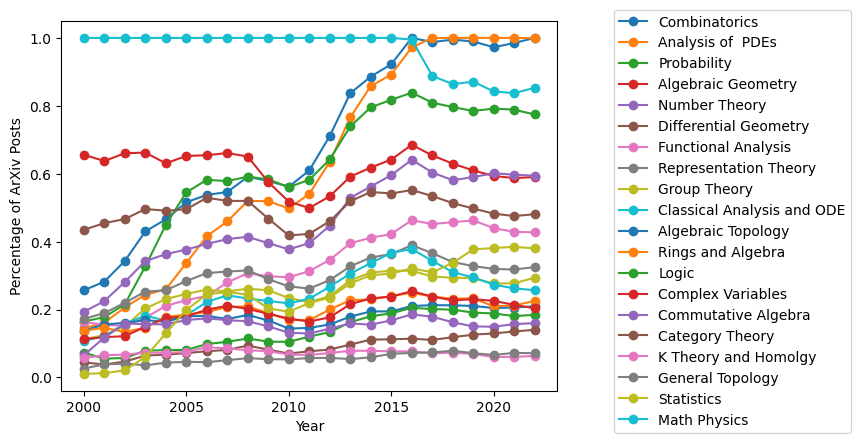
This was a simple count of how many papers were released on the arxiv under each tag each year. This was carried out in python and the code can be found here .

Justified True Belief

It always annoyed me how Justified True Belief (JTB) was introduced as a response to the classical conception of knowledge; you can go and read the texts and they never mention it, Plato as explicitly as Plato does rejects it. This framing however is pushed and its prevents a proper analysis of what the tradition actually was. I found a good article discussing how this myth came to be, what the actual tradition may have been and just what Gettier was responding to (since it cannot have been the traditional conception of knowledge):

Dutant, Julien. “THE LEGEND OF THE JUSTIFIED TRUE BELIEF ANALYSIS.” Philosophical Perspectives, vol. 29, 2015, pp. 95–145. JSTOR, https://www.jstor.org/stable/26614563. Accessed 10 Jan. 2024.

Model Theory

I had a similar experience with model theory; it seems on the face of it to have principles that are neccissary for it to function formally that are seldom recognised and even less often talked about. The basic problem is this; there is a meta-theory and a subject theory. In some instances people want to talk about them being the same, they will use words like "coding" etc. To beleive the results proved in the meta about the coding of the meta we need to beleive in a principle of externalisation, this cannot be gotten from the theory. If youre a platonist this might not be a problem for you I suppose (Godel was), the languages are talking about the same platonic objects. Well I found some discussions on the matter that I just want to collect here for my own sanity:

https://cs.nyu.edu/pipermail/fom/2020-January/021874.html : An email between Timothy Chow and Detlefsen discussion the extra unspoken principle (in the context of Godels theorem)
Hilbert's Program: An Essay on Mathematical Instrumentalism, vol. 182 of the Synthese Library, D. Reidel Publishing Co.,1986, ISBN 978-94-015-7731-1 : Detlefsen's book on the problem, and how it effects the commonly touted defeat of Hilberts program
https://math.stackexchange.com/q/4835354/1273463 : A pretty confused post I made on the matter.
https://math.stackexchange.com/a/4360940/1273463 : Points out that the meta-theory can be much weaker than the subject theory.
https://math.stackexchange.com/a/3574484/1273463 : A good defense of the "forget about foundations" approach given by Kruckman, the best statement is in the comments

"Mathematics is a social enterprise, which is carried out in natural language. Vanishingly few theorems have actually been formalized in ZFC. Now to make mathematics a coherent enterprise, we have to agree on what counts as a proof, and the common consensus is we accept a proof if it can in principle be formalized in ZFC. Those who care put in the work to carefully understand what can be formalized but the majority just pick up the intuition for this as they get socialized into the mathematical community."

is true but not helpful if you happen to be one of the people who want to put in the work.
https://mathoverflow.net/q/22635/519939 : A better articulation of my question. The answers by Timothy Chow and Peter LeFanu Lumsdaine are fantastic.
https://mathoverflow.net/q/248965/519939 : Is a very interesting discussion with the most relevant answers being by Burak
Kunen writes "The metatheory consists of what is really true." (1980, p.7, his emphasis) as part of a longer explanation. Try to figure out what axiomatic theory that is! His goal is to avoid having to pin himself down - he wants the reader to be able to insert their own metatheory on top of his exposition.
https://mathoverflow.net/q/437195 : Some interesting discussions in the comments

Good Exposition

Timothy Chow in his article on forcing expresses his idea of an "open exposition problem". I think that his remarks about what makes a good exposition are seldom instantiated in the mathematical literature, I would like to record them here as a reminder to myself what I should aim for when giving talks and presentations and writing exposition.

All mathematicians are familiar with the concept of an open research problem. I propose the less familiar concept of an open exposition problem. Solving an open exposition problem means explaining a mathematical subject in a way that renders it totally perspicuous. Every step should be motivated and clear; ideally, students should feel that they could have arrived at the results themselves. The proofs should be “natural” in Donald Newman’s sense (Analytic Number Theory, Springer-Verlag, 1998): This term . . . is introduced to mean not having any ad hoc constructions or brilliancies. A “natural” proof, then, is one which proves itself, one available to the “common mathematician in the streets.”

Some other things to bear in mind are

Every time you name something, explain why; if it is a later result reference it, if it is historical, annological, explain it.
Every time you make a simplifying assumption explain how the general case can be reduced to it; if it cannot remark on this as well, it is ok to make assumptions just so we can get an idea, but be clear about WHY we make the assumption.

○ ○